인공지능 기말고사 대비

8강 neural network (신경망)

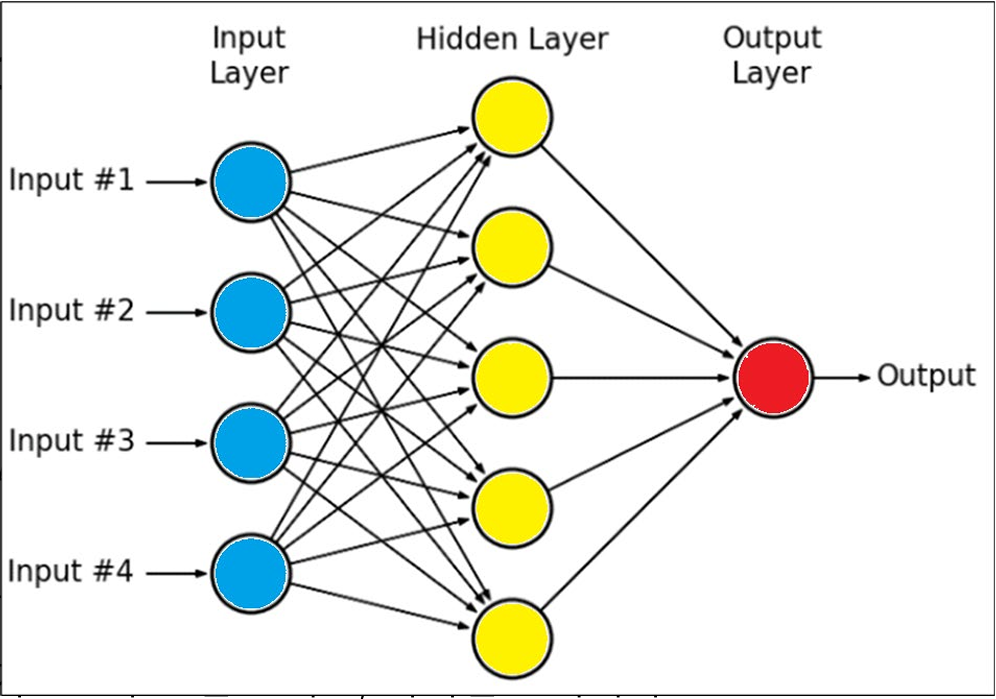
input : data데이터

input layer(입력층) : no activation (활성화되지 않는다) 데이터 전달만함

hidden layer(은닉층) : 활성함수를 통해, 활성 여부 전달(중간에 있는 층이 몇개든 다 은닉층이다.)

output layer : 활성함수를 통해 답일 확률을 계산

output : 답을 유저가 알아듣도록 재조립함, 추론한 답과 실제 답을 비교한다(loss function)

순전파: 입력이 신경망을 거쳐서 출력값으로 변환되는 과정이다.

역전파 : 출력오차를 기반으로 w와 b를 조정하는 과정

gradient는 loss가 w/b에 따라 얼마나 변화하는지를 나타내며, 이를 따라 w를 업데이트하면 loss가 줄어들도록 학습 가능

 

퍼셉트론 : 여러 입력(input,data)을 받아서, 가중치를 곱해서 더하고 임계값을 넘으면 1,아니면 0을 출력하는 모델, 선형분리기 (하나의 2D에서 직선을 찾는 방법)

ㄴ 가중합 : f=w1​x1​+w2​x2 ​+⋯+wn​xn+b (w: weight, b: bias)

 

텐서 :

 

9강 neural network , activation function (신경망, 활성함수)

relu/ sigmoid

bias(편향) : 마지막에 더하는 것, 기준선, 임계값, 0이 아닌 출발점

weight(가중치) : 각 선들이 의미하는 값, 각 입력이 결과에 얼만큼 영향력을 가지는지 결정

학습 = loss(손실)을 최소로 만드는 w,b를 찾는과정

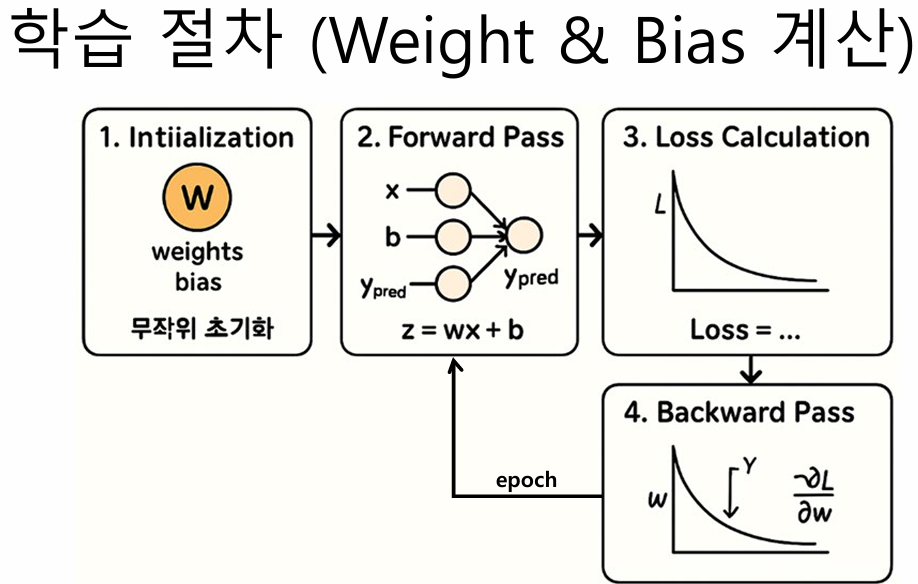
1. 초기화 : w와 b를 무작위 혹은 작은 값으로 시작 (모델은 아직 아무것도 모른다.)

2. 순전파 forward pass : 현재 모델 기준으로 예측값을 계산한 것 ( 입력값x에w, b를 곱하고 합산→ z = w·x + b (Perceptron))

3. loss계산 : 실제값과 예측값 비교 bceloss(얼마나 틀렸는지 점수 매기기)

4. 역전파 backward pass : 지금 손실이 크니까 값을 조정해주자

ㄴ Loss를 w, b에 대해 미분 → gradient (기울기)구함

ㄴㄴ gradient = 이 방향으로 w, b를 움직이면 loss가 줄어듬 , gradient 가 0이면 멈춤 , gradient 가 크면 많이 움직임

5. weight와 bias 업데이트 (기울기 감소 gradient descent) : 반복하면서 손실이 점점 줄어들고 정답에 가까워지도록 w,b 조정

6. 반복(에폭) : 모든 데이터를 여러번 순전파, 역전파 하면서 w,b를 계속 업데이트, 최적화가 끝나면 loss가 최소화

 

활성화 함수 : 입력값을 변환하여 출력값을 생성

sigmoid : S자 모양이여서 시그모이드라고 부른다.

가중치 값에 따라서는 중간에서 만나고 작을 수록 평평하고, 편향값에 따라서는 양끝에서 만나고 작을수록 아래위치한다. 중가평

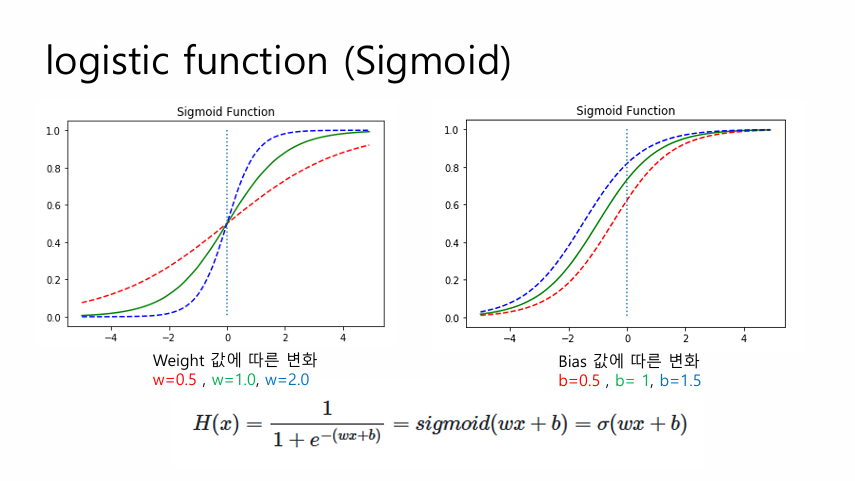
시그모이드 미분하면 = y(1-y)

sigmoid+BCE 

= gredient계산과 오차 전파가 가능하고 분류 성능을 최적화가능하게 한다.

 

오차제곱합 SSE

오차의 제곱을 합산한 값으로 대표적인 loss 계산법, 오차가 클수록 높은값출력

손실을 수치로 측정하면 출력과 정답 간 오차 크기를 정량화 할 수 있다. 이값을 기반으로 역전파에서 기울기를 계산하고 w,b를 조정하면 학습이 가능하다.

10강 Neural Network, Loss Optimize Function (신경망, 손실함수.최적화함수)

bceloss/ optim.adam(model.parameters(), lr=0.01)

손실함수 (BCE, binary cross entropy)

: 이진분류를 할때 사용하는 손실함수, 정답(0/1)과 모델이 예측한 확률 (0~1)사이의 부족한 정도를 로그로 재는 손실

ㄴ 로그를 쓰는 이유 : 잘못 확신한 예측에 큰 패널티를 주기 위해서

이진분류의 특성상 y값이 0또는 1이 나오기 때문에 위와 같은 식을 구현하여 loss값을 추출할 수 있게 됨

 

최적화함수1(SGD, stochastic Gradient Descent)

확률적 경사 하강법, 가장 빨리 내려갈 것 같은 방향(경사)로 조금씩 움직이며 학습하는 방법

한번 업데이트할때 데이터1개만 사용하는데 이유는 너무 느리기때문에

장점 : 메모리를 적게쓰고 빠름, 대규모 데이터셋에 적합

단점 : 경사방향이 들쭉날쑥함, 진동 많음

 

최적화함수2(Adam, Adaptive Moment Estimation) 적응적 모멘트 추정